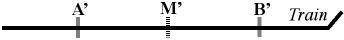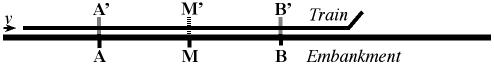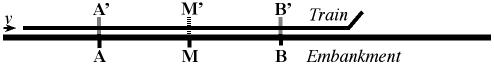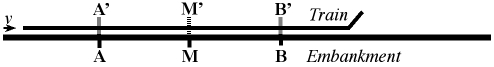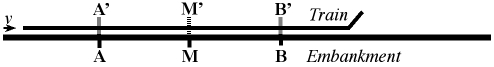The
Einstein Light Motion Paradox
Bob
Kroepel
Copyright
© 2012
Lakeside Studios
20 South Shore Road
New Durham, NH USA 03855
Table of Contents
- Introduction
- Simultaneity in Physics
- Einstein's Conception of Simultaneity
- The Concept of
a Reference Frame
- The Concept of a Reference Body
- Chronological Sequences (Time Sequences)
- Gross Time Sequences
- Precise Time Sequences
- Sequences
1, 1b & 1c and Movie 1c
- Sequence 1
- Sequence 1b
- Sequence
1c
- Movie 1c
- Sequences 2, 2b & 2c and Movie 2c
- Sequence 2
- Sequence 2b
- Sequence
2c
- Movie 2c
- Comparing Sequences 1, 1b,
& 1c & Movie 1c vs Sequences 2, 2b, & 2c &
Movie 2c
- The Problem: The Einstein Light Motion
Paradox
- Relative
Velocity (RV) Facts
- Velocity in Physics
- Speed and Direction
- Relative Velocities (RVs) and
Measured Velocities (MVs)
- Relative Velocities
- Measured Velocities
- Approach and Departure Velocities
- The Maximum RV
- The Minimum Velocity
- Velocities inre Einstein's Fig. 1
- Relative Velocities and the
Einstein Light Motion Paradox
- Simultaneity
and The General Principle of Relativity
- The Concept of Time
- The Temporal Principle
- The Time-Interval
- The Timerate
- Timepoints
- Timelines
- Timecounts
- The Temporal Process
- Time: Never Destroyed nor Created
- Time: Infinite in Duration
- The Essence of Time: The
Time-Interval
- The Two Types of Clocks
- The Two Types of Time
- Distortable Time: Local Time
- The Continuum of Local Time (CoLT)
- Adjustable/Non-Distortable Time:
Absolute Time
- The Continuum of Absolute Time
(CoAT)
- The Two Types of Adjustable Clocks:
Radio Clocks & Inertial Clocks
- Radio Clocks
- Inertial Clocks
- Simultaneities, Timepoints, and
Time-Stamps
- The Moving Observer Illusion (MOI)
- Summary: The
Einstein Light Motion Paradox
Introduction
Simultaneity in Physics
In physics, simultaneity is defined as
the occurrence of two or more events at the same timepoint.
Einstein's
Conception of Simultaneity
In Relativity, 1961 edition,
Chapter
IX, Einstein showed that when light is used to determine the
simultaneity of events the relativity of different reference frames and
observers will prompt an observer in one reference frame to report
detecting proof that two events occurred simultaneously while another
observer in another reference frame will report detecting proof
that the two events did not occur simultaneously.
Einstein:
[Paragraph 1] Up to now our considerations have been referred to a
particular body of reference, which we have styled a “railway
embankment.” We suppose a very long train travelling along the rails
with the constant velocity v and in the direction indicated in Fig. 1.
People travelling in this train will with advantage use the train as a
rigid reference-body (co-ordinate system); they regard all events in
reference to the train. Then every event which takes place along the
line also takes place at a particular point of the train. Also the
definition of simultaneity can be given relative to the train in
exactly the same way as with respect to the embankment. As a natural
consequence, however, the following question arises:
[Paragraph 2] Are two events (e.g. the two strokes of lightning A and B) which are
simultaneous with reference to the
railway embankment also simultaneous relatively to the train? We shall
show directly that the answer must be in the negative. [Einstein, Relativity, 1961
edition, Chapter
IX]
Inre Relativity, Einstein
proposed a unique way to determine the simultaneity of two events.
Einstein presented in Chapter IX of Einstein's Relativity,
1961 edition, the Fig. 1 Einstein Railroad Drawing:

Fig. 1
For the purpose of clarity inre this article, the Einstein Railroad
drawing has been redrawn thus:
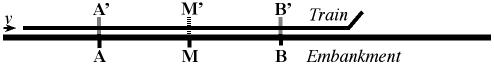
Fig. 1 (Redrawn)
The distinction of Events A' & B' from Events A & B and
distinction of the length A'-B' from the length A-B are made ...
(A) to distinguish the lightning strikes that are Events A & B inre
(in regards, in relation to, relative to, or about) the Embankment as
Events A & B and inre the Train as Events A'
& B',
(B) to distinguish Lightrays A & B from Events A & B from
Lightrays A' & B' from Events A' & B',
... and ...
(C) to distinguish the length A-B inre M and the Embankment from the
length A'-B' inre M' and the Train,
... thus showing better the causal and coincidental relationships inre
the M & Embankment reference frame K and the M' & Train
reference frame K', especially to show howitiz that the lengths A'-B',
A'-M' and B'-M' travel with the Train, and howitiz that because the
Train has been in-motion at an unspecified measured velocity (MV) that
the lengths A'-B', A'-M' and B'-M' are NOT space-contracted.
Einstein, in Paragraph 1, stated that ...
... the Railway Embankment is one reference frame ...

Einstein RR Embankmkent
... and
...
... the Railway Train is another reference frame ...
Einstein RR Train
The Concept of
a Reference Frame
In this article, a reference frame
is a co-ordinate system consisting of three axes, the x-axis, the
y-axis, and the z-axis, extending as straight lines from a common
origin, within which entities which are at-rest, motionless, no
relative velocity, (RV = 0.00c, as explained below), are described as
being in the reference frame.
For every possible velocity
(speed + direction, as explained below), there is a separate reference
frame. Reference frames are distinguished from other reference frames
by their velocities (speeds + directions).
In this article, when necessary, the Embankment is described as
reference frame K and the Train is described as reference frame K'.
Because M is motionless inre the Embankment, M and the Embankment are
in the same reference frame, K; because M' is motionless inre the
Train, M' and the Train are in the same reference frame, K'.
The Concept of a Reference Body
In this article, a reference body
is an entity to which a reference frame is attached with its origin at
the Entity's center of mass (CoM) with the reference frame's
co-ordinate system's x-axis aligned parallel to the Entity's direction
of motion.
In Fig. 1, the Embankment has a CoM to which the reference frame K
co-ordinate system can be attached, therefore the Embankment is a
reference body, and thereby the Embankment reference body can also be
labeled K, and the Train has a different CoM to which the reference
frame K' co-ordinate system can be attached, and thereby the Train
reference body can also be labeled K'.
The combination of a reference frame with a reference body means that
in essence a reference frame and reference body are the same inre being
a point-of-view (PoV) from which observations and measurements can be
made and within which the laws of physics are the same (a natural
causal relationship observed to have occurred inre one reference
frame/body is expected to be observed to occur inre any and all other
reference frames/bodies (explained below in Simultaneity and The
General Principle of Relativity).
---
In the redrawn Fig. 1, Events A & B have been augmented by the
letters A' and B' to show how it is that Events A & B inre the
Embankment also occurred as Events A' & B' inre the Train, and
how it is that the length A-B inre the Embankment is identical to the
length A'-B' inre the Train.
In this article, the phrase Events A
& B can mean both
Events A & B and Events A' & B'.
The length A-B inre the Embankment is identical in length to the length
A'-B' inre the Train. Whereas the Train had been in-motion inre the
Embankment prior to Events A & B (A' & B'), the fact that
length A-B is identical to length A'-B' means there is no
length-contraction inre the length A'-B' inre the Train.
In the drawings in this article, the length A-B and thus the length
A-M-B does not move inre the Embankment but the length A'-B' and thus
the length A'-M'-B' moves with the Train.
The following comments inre Fig. 1 by Einstein in Paragraph 3 of
Chapter IX of Relativity
present a sequence of
events as observed by M on the Embankment.
Einstein:
[Paragraph 3] When we say that the
lightning strokes A and B are
simultaneous with respect to be embankment, we mean: the rays of light
emitted at the places A and B, where the
lightning occurs, meet each other at the mid-point M of the length A -> B of the
embankment. But the events A and B also correspond
to positions A and B on the train.
Let M' be the
mid-point of the distance A -> B
on the travelling train. Just when the flashes [as judged from the
embankment] of lightning occur, this point M'
naturally coincides with the point M, but it moves towards the
right in the diagram with the velocity v
of the train.
If an observer sitting in the position M'
in the train did not possess this velocity, then he would remain
permanently at M, and the light rays emitted
by the flashes of lightning A and B would reach him simultaneously, i.e. they would meet him just where he
is situated.
Now in
reality (considered with reference to the railway embankment) he [M']
is
hastening towards the beam of light coming from B,
whilst he [M'] is riding on ahead of the
beam of light coming from A.
Hence the observer [M'] will see the beam of
light emitted from B
earlier than he [M'] will see that emitted
from A.
Observers [including M'] who take the railway
train as their reference-body must
therefore come to the conclusion that the lightning flash B
took place earlier than the lightning flash A.
[Einstein, Relativity, 1961
edition, Chapter
IX].
Of special note inre Paragraph 3:
1. "[T]he rays of light
emitted at the places A and B, where the
lightning occurs, meet each other at the mid-point M of the length [A-B] of the
embankment [and] the events A and B
also correspond to positions A and B
on the train".
Comment: The distance
(length) A-B is the same for both the Embankment and the train (A-B =
A'-B'). The train is in-motion prior to the occurrences of Events A
& B, therefore the x-axis length-contraction inre the Train would
have occurred prior to the Events A & B, and, therefore, the length
A-B is the same for both the Embankment and the Train (A-B = A'-B'),
i.e. there is no length-contraction inre the length A'-B' inre the
Train.
2. "Now in
reality (considered with reference to the railway embankment) [M']
is
hastening towards the beam of light coming from B
[and] [M'] is riding on ahead of the
beam of light coming from A".
Comment: The relative
velocity (RV) inre M' and the Lightray B' from Event B' is greater than
1.00c because the velocity of Lightray B' is to be added to the
velocity of M' (and the Train) by the equation ...
... RV = MV1 + MV2 ...
... where ...
... RV = Relative Velocity;
... MV = Measured Velocity;
... MV1 = Measured Velocity of Lightray B';
... MV2 = Measured Velocity of M'.
The MV1 of Lightray B' is assumed to be the speed of light in vacuo (in a subvolume of space
which is devoid of matter-energy, m/e, including electromagnetism and
gravity), i.e. the MV1
of Lightray B' is assumed to be 1.00c; the MV2 of M' is not given but
we can assume that because M' is an entity comprised of m/e that he
[M'] will be in-motion at an MV2 < 1.00c but at an MV2 > 0.00c.
The RV inre M' and Lightray A' from Event A' is less than 1.00c because
the velocity of Lightray A' is to be subtracted from the velocity of M'
(and the Train) by the equation ...
... RV = MV1 - MV2 ...
... where ...
MV1 = Measured Velocity of Lightray A';
MV2 = Measured Velocity of M'.
3. "[M']
will see the beam of light emitted from B
earlier than he [M'] will see [the beam of
light] emitted
from A".
Comment: M' could not
'see' (detect, observe) Lightray B' from Event B' "earlier" than he
[M'] would 'see' Lightray A' from Event A' if the RV of Lightray B'
& M'
was 1.00c and the RV of Lightray A' & M' was also 1.00c.
If the MV of Lightray B' were to equal (be the same as) the MV of
Lightray A' and therefore the MV of Lightray A' would be 1.00c and the
MV of Lightray B' would also be 1.00c, then Lightrays A' & B' would
strike M' simultaneously (at the same timepoint) and therefore he [M'],
will
'see' Lightray A' at the same timepoint he [M'] will 'see' Lightray B',
and
therefore he [M'] would be justified in concluding and reporting that
Events A' & B' occurred simultaneously (at the same timepoint).
4. "Observers [including M'] who take the railway
train as their reference-body must
therefore come to the conclusion that the lightning flash B
took place earlier than the lightning flash A."
Comment: Whereas
Einstein stated/stipulated that the Events A & B ( and Events A'
& B') occurred simultaneously for both
the Embankment and the Train, and, theoretically, if the speed of light
is the same for all observervs, which, interpreted, means that Lighrays
should have traveled past both M
and M' at 1.00c, then both M and M' should have detected Lightrays
simultaneously (at the same timepoint) and therefore both M and M' should have judged and reported
that Events A & B (and Events A' & B') occurred simultaneously.
But Einstein does not say so
in the #4 quote cited.
Instead, in the quote #4 cited, he says that observers inre the Train
reference frame/body should detect Lightray B' before detecting
Lightray A', and that means M', being obviously an observer inre the
Train reference frame/body, along with any other observers inre the
Train reference frame/body, should have detected Lightray B' before
detecting Lightray A'.
Inre the light motions inherent in Fig. 1, the concept of a chronological sequence, or time sequence, is critical.
Chronological Sequences (Time
Sequences)
A chronological
sequence is a time sequence or
listing of the occurrences of events at timepoints (time
marks) on a timeline
(continuum of time, a history, or record, of events).
Gross Time Sequences
A gross time
sequence
presents a chronological sequence in terms of the
timepoints at which specific events occurred without regard for—without
the requirement for—equivalent durations between timepoints nor
equivalent durations of timepoints.
Ex(ample): In the game of baseball, there is no game clock which keeps precise
timepoints on a timeline because the game is played by a total of nine
innings and the duration of an inning typically is unpredictable and
therefore variable, with the result that events (home runs, triples,
doubles, singles, strikeout, double-plays, triple-plays, runs scored,
etc.) are listed by innings in a gross time sequence.
Precise Time Sequences
A precise time
sequence presents a
chronological sequence in terms of
equiduration and equidistant timepoints (timepoints of equal duration
separated by equal durations) at
which specific events occurred.
Ex: In some games, including football, basketball, and hockey, game
clocks are used and events are often listed according to the game clock
timepoint at which they occurred. In football, the game clock is split
into four quarters of fifteen minutes, fifteen timepoints, each. Events
in a football game (touchdowns, field goals, passes completed, pass
intercepted, runs scored, ... etc.) can be listed as occurring at
minutes on the game clock. A game clock often differs from a 24-hour
clock because of timeouts, or pauses in the game action, which cause
timekeepers to stop the game clock. Nevertheless, when the game clock
is running, the durations of timepoint (minutes) are equal and the
durations between the minutes are also equal.
Ex: A 24-hour clock is a standard clock for most people, in which there
are twenty-four hours divided into 60 minutes per hour divided into 60
seconds per minute, and if a 24-hour clock is operating properly, then
the durations of the seconds, minutes, hours, etc., are equal, and the
durations between the ticks
of the seconds, minutes, hours, etc., are also equal. The USNO (US
Naval Observatory), the US NIST (US National Institute of Standards and
Technology), and the BIPM (Bureau Internationale des Poids et Mesures,
in France) use adjustable clocks which are the standard clocks which
are used to maintain the standard second and which are therefore the
time standard for civilians, military personnel, and scientists wherein
the durations of seconds are equal and the durations between seconds
are equal. The US GPS nav system's tming system consists of a master
clock which controls the timerates of slave clocks in the GPS
satellites; the GPS master clock is synchronized with the USNO standard
clocks and thereby broadcast the USNO standard time to any individuals
and organizations whose time standard requirements are satisfied by the
precision of the USNO standard clocks.
Sequences
1, 1b & 1c and Movie 1c
Sequence 1 is a paraphrase of Paragraph 3 of Chapter IX of Relativity in which the sequence of
events inherent in Fig. 1 as described by Einstein in Paragraph 3 are
presented in a numerical sequence (numbered sequence).
Sequence 1
1. Lightning strikes A & B; Events A & B occur simultaneously
inre distance A-B
inre both the Embankment & the Train;
2. Light from B' strikes M' (M' reports detecting Lightray B' from
Event B');
3. Light from A and B strike M (M reports detecting Lightrays A & B
from Events A
and B and his judgment that Events A & B occurred simultaneously);
4. Light from A' strikes M' (M' reports detecting Lightray A' from
Event A' and his judgment that Events A' & B' occurred
non-simultaneously).
Sequence 1 is a gross
time sequence.
A gross time
sequence
presents a chronological sequence in terms of the
timepoints at which specific events occurred without regard for—without
the requirement for—equivalent durations between timepoints nor
equivalent durations of timepoints.
The gross time sequence for Sequence 1 is presented as Sequence
1b, wherein T = Timepoint
and there are four timepoints, T1, T2, T3, & T4.
Sequence 1b
NOTE: T = Timepoint
1. T1: Lightning strikes A & B; Events A & B occur
simultaneously inre distance A-B
inre both the Embankment & the Train;
2. T2: Light from B' strikes M' (M' reports detecting Lightray B' from
Event
B');
3. T3: Light from A and B strike M (M reports detecting Lightray A
& B from
Events A
and B and his judgment that Events A & B occurred simultaneously);
4. T4: Light from A' strikes M' (M' reports detecting Lightray A' from
Event
A' and his judgment that Events A' & B' occurred
non-simultaneously).
There are four
timepoints in the gross time sequence which is Sequence 1b; these
timepoints are not necessarily of equal durations nor are the durations
between them necessarily of equal durations.
The following drawings illustrate the causal and
coincidental
relationships inre the movements of lightrays from Events A & B,
the motion of the Train, and the motion of M' relative to M and the
Embankment illustrated in Fig. 1, in Sequence 1 and in Sequence 1b at
Timepoints T1, T2, T3, & T4.
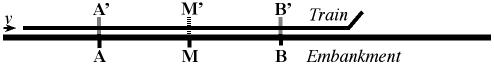
1. T1: Events A & B occur simultaneously inre the Embankment and
the
Train.

2. T2: Light from B' strikes M'.

3. T3: Light from A & B strike M.

4. T4: Light from A' strikes M'.
Sequence 1c, is a precise time
sequence in which the causal and
coincidental events inherent in Einstein's Fig. 1 are presented as
timepoints T1-T16.
1. T1:
Einstein RR (Sequence 1c: Movie 1c)

2. T2: Einstein RR (Sequence 1c: Movie 1c)

3. T3: Einstein RR (Sequence 1c: Movie 1c)

4. T4: Einstein RR (Sequence 1c: Movie 1c)

5. T5: Einstein RR (Sequence 1c: Movie 1c)

6. T6: Einstein RR (Sequence 1c: Movie 1c)

7. T7: Einstein RR (Sequence 1c: Movie 1c)

8. T8: Einstein RR (Sequence 1c: Movie 1c)

9. T9: Einstein RR (Sequence 1c: Movie 1c)

10. T10: Einstein RR (Sequence 1c: Movie 1c)

11. T11: Einstein RR (Sequence 1c: Movie 1c)

12. T12: Einstein RR (Sequence 1c: Movie 1c)

13. T13: Einstein RR (Sequence 1c: Movie 1c)

14. T14: Einstein RR (Sequence 1c: Movie 1c)

15. T15: Einstein RR (Sequence 1c: Movie 1c)

16. T16: Einstein RR (Sequence 1c: Movie 1c)
Movie 1c
Movie 1c: http://www.bobkwebsite.com/einsteinrr1c.mov
Sequence 1, Sequence 1b and Sequence 1c are paraphrases of Einstein’s
description in Paragraph 3 of Chapter IX of Relativity of the motions of
Lightrays from
Events A & B (and Events A' & B') in relation
to M, the Embankment, M', and the Train which are inherent in Fig. 1.
Sequences 2, 2b & 2c and Movie 2c
Sequence 2 is a gross time sequence which describes the motions of
Lightrays from Events A & B in relation to M, the Embankment, M',
and the Train when the length A-B (A'-B') moves with the M' and the
Train and Lightrays A' & B' travel at 1.00c towards M'.
Sequence 2
1. Events A & B occur simultaneously inre the Embankment and the
Train.
2. Lightrays from A & B strike M and M' simultaneously (both M
& M'
report detecting Lightrays from Events A & B simultaneously and
their judgments that Events A & B occurred simultaneously).
NOTE: Because Lightrays from A &
B
struck M and M' simultaneously, there is no need for a T3 or a T4 inre
Sequence 2.
Sequence 2b is a gross time sequence which describes the motions of
lightrays from Events A & B in relation to M, the Embankment, M',
and the Train when the length A-B (A'-B') moves with the M' and the
Train at timepoints T1, T2, T3, & T4.
Sequence 2b
1. T1: Events A & B occur simultaneously inre the Embankment and
the
Train.
2. T2: Lightrays from A & B strike M and M' simultaneously (both M
& M'
report detecting Lightrays from Events A & B simultaneously and
their judgments that Events A & B occurred simultaneously).
NOTE: Because Lightrays from A &
B
struck M and M' simultaneously, there is no need for a T3 or a T4 inre
Sequence 2b.
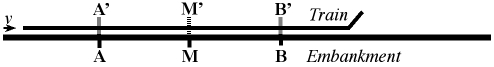
1. T1:
Einstein RR (Sequence 2b)

2. T2: Einstein RR (Sequence 2b)
Because Sequence 2b is a gross time sequence, there are only two
timepoints, T1 & T2.
When the Lightrays A' & B' from Events A' & B' travel with
distance A-B (A'-B') and M' and the Train, then Lightrays A' & B'
travel towards-past-away-from M' at 1.00c while Lightrays A & B
also travel
towards-past-away-from M at 1.00c.
Sequence 2c is the precise time sequence of events at timepoints T1-T8
when the length
A-B (A'-B') moves with M' and the Train and Lightrays A' & B' from
Events A & B also move with M' and the Train.
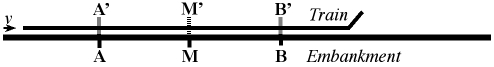
1. T1:
Einstein RR (Sequence 2c: Movie 2c)

2. T2: Einstein RR (Sequence 2c: Movie 2c)

3. T3: Einstein RR (Sequence 2c: Movie 2c)

4. T4: Einstein RR (Sequence 2c: Movie 2c)

5. T5: Einstein RR (Sequence 2c: Movie 2c)

6. T6: Einstein RR (Sequence 2c: Movie 2c)

7. T7: Einstein RR (Sequence 2c: Movie 2c)

8. T8: Einstein RR (Sequence 2c: Movie 2c)
Movie 2c illustrates the specific sequence of events when the length
A'-B' moves with M' and the Train and Lightrays A' & B' from Events
A
& B also move with M' and the Train.
Movie 2c
Movie 2c: http://www.bobkwebsite.com/einsteinrr2c.mov
Comparing Sequences 1, 1b,
& 1c & Movie 1c vs Sequences 2, 2b, & 2c &
Movie 2c
Here are T1 and T3 from Sequence 1b and T1 and T2 from Sequence 2b:
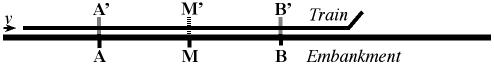
Sequences 1b & 2b: T1: Events A & B Occur Simultaneously inre
the
Embankment and the Train.

Sequence 1b:
T3: Lightrays from Events A & B strike M Simultaneously.

Sequence 2b: T2: Lightrays from Events A & B Strike M and M'
Simultaneously.
Sequence 1, Sequence 1b and Sequence 2b start at T1 with Events A &
B occurring simultaneously inre the Embankment and the Train.
Inre
Sequence 1, at T3, when light travels at RV = 1.00c inre M & the
Embankment and at RV ≠ 1.00c inre M' & the Train, Light from B' has
already struck M' and Light from A & B strike strike M
simultaneously.
Inre Sequence 2b, at T2, when light travels at RV =
1.00c inre M & the Embankment and M' & the Train, then Light
from A & B strike M and M' simultaneously.
Therein lies the Einstein Light Motion Paradox: For Events A &
B to be non-simultaneous inre M' & the Train in Sequence 1b, then
the RV of light inre M & the Embankment ≠ the RV of light inre
M' & the Train; for Events A & B to be simultaneous inre M
& the Embankment AND inre M' & the Train, then the RV for
light inre M & the Embankment = RV for light inre M' & the
Train.
The Problem: The Einstein Light
Motion Paradox
Problem:
In Paragraph 3, Einstein
stated/stipulated clearly that Events A & B (and Events A' & B'
in the redrawn Fig. 1) occurred simultaneously inre both the
Embankment—reference frame K and the Train—reference frame K', but
then, also in Paragraph 3, he stated that, as observed from either K or
K', M or M' would detect Lightrays at different timepoints and
therefore there is a relativity of simultaneity that conflicts with the
objective fact that Events A & B (and Events A' & B' in the
redrawn Fig. 1) occurred simultaneously inre K & M and inre K'
& M'.
If Events A & B (and Events A' & B' in the redrawn Fig. 1)
occurred simultaneously inre both the Embankment/reference frame K and
the Train/reference frame K', and if the motions of the Lightrays A, B,
A', & B' were RV = 1.00c for both
M in K and M' in K', as
described
by Einstein's light motion equation, RV = (MV1 + MV2)/(1 + MV1 x MV2/C2),
then both M and M' should have reported detecting
Lightrays from
Events A & B (and A' & B' in the redrawn Fig. 1)
simultaneously, at #2 in Sequence 2 and at #2. T2 in sequence 2b.
Because of their relative velocity difference (because their reference
frames/bodies have different MVs and therefore they have different
MVs), M and M', at least in theory, ought to observe each other
detecting Lighrays from Event A & B at different timepoints and
conclude that there is a relativity of simultaneity which ought to mean
that, if true, then Events A & B did not occur simultaneously inre both M in K and
M' in K'.
The Problem herein is the Einstein Light Motion Paradox wherein there
is an objective fact of simultaneity (Events A & B occurred
simultaneously—at the same timepoint—inre K & M and K' & M')
which conflicts with the concept of the relativity of simultaneity
(wherein because of their relative velocity difference M and M' would
detect Lightrays at different timepoints and thereby judge that the
Events A & B did not occur simultaneously).
Relative
Velocity (RV) Facts
Velocity in Physics
In physics, velocity is the
combination of an Entity's speed and direction of motion.
Speed and Direction
Speed and direction are two different
characteristics of motion (another characteristic is the change of speed, particularly the rate of change of speed, caused by
acceleration or deceleration forces; another characteristic is change of direction, particularly
the rate of change of direction,
caused by acceleration and deceleration forces).
Speed is motion without regard
for direction while direction
is motion without regard for speed.
Although speed and direction are interconnected in the concept of
velocity, when either necessary or otherwise convenient, it is logical
and therefore possible for people to refer to speed in any
direction and thereby disregard speed in a specific direction (someone
could talk about the top speed of a car regardless of direction) or to
refer to direction and thereby disregard direction with any specific
speed (a person could travel in a direction at any speed).
Relative Velocities (RVs) and
Measured Velocities (MVs)
Relative
Velocities
Relative velocities
(RVs) are the combinations or differences inre the measured velocities
(MVs) of Entities.
Relative velocities (RVs) occur when Entities have different
measured velocities (MVs).
A relative velocity
(RV) is the combination or difference inre the measured velocities
(MVs) of two Entities.
Measured Velocities
A measured
velocity (MV) is the velocity of an entity as measured in
relation to a reference point or object (entity). In Fig. 1, the v
of the Train (and M') is an MV inre the Embankment, or inre M as M
stands on and is thereby motionless inre the Embankment. In that
regard, an MV is an RV because it is the difference between the
velocity of an entity in relation to (inre) the velocity of a reference
point.
A relative velocity (RV) is either ...
(1) the combination of the measured
velocity (MV) of one entity (MV1) and the measured velocity of another
entity (MV2) described by RV = MV1 + MV2,
... or ...
(2) the difference between the measured
velocity (MV) of one entity (MV1) and the measured velocity of another
entity (MV2) described by RV = MV1 - MV2.
Approach and Departure Velocities
In aviation, a relative velocity (RV) can be described as an approach velocity (herein referred
to as an approach relative velocity,
or ARV) or as a departure velocity
(herein referred to as a departure
relative velocity, or DRV).
NOTE: In aviation,
approach-departure velocities are generally restricted to aircraft inre
fixed locations on the ground (the Earth's surface), but for the theory
of relative velocities approach-departure velocities can be described
inre entities in-motion and/or positions in space (spacepoints) in
addition to fixed locations on the ground.
An ARV occurs (A) when two Entities approach—move towards—each other
from opposite directions or (B) when one Entity moves towards another
Entity in the same direction; a DRV occurs (A) when two Entities
depart—move away—from each other in opposite directions or (B) when one
Entity moves away from another Entity in the same direction.
Fact: An ARV can be the sum of two Lightrays traveling in
opposite directions and parallel to each other with the MV1 of a
Lightray
traveling
at 1.00c and the MV2 of an Entity traveling less than 1.00c, by RV =
MV1 + MV2, without either the Lightray or the Entity traveling faster
than 1.00c.
Fact: A DRV can be the difference between the MV1 of a
Lightray traveling at 1.00c and the MV2 of an Entity traveling less
than 1.00c, by RV = MV1 - MV1.
The Maximum RV
Fact: The maximum RV would be the ARV inre two Lightrays, Lightray A
& Lightray B, which are
approaching each
other from opposite directions and are traveling parallel to each other
and each Lightray is traveling at MV = 1.00c or the DRV inre two
Lightrays, A & B, which are departing from each other by traveling
parallel to each other in opposite directions at 1.00c each.
The RV equation for the maximum ARV is RV = MV1 (Lightray A) + MV2
(Lightray
B), for an RV = 1.00c + 1.00c, or RV = 2 x 1.00c or 2.00c without
either
Lightray traveling
faster than 1.00c.
The RV equation for the maximum DRV is DRV = MV1 + MV2 = 1.00c + 1.00c
= 2 x 1.00c = 2.00c without either Lightray traveling faster than 1.00c.
The Minimum Velocity
Fact: The minimum RV would be the RV inre two Entities that are at-rest
in a single reference frame or on a single reference body, described by
RV = MV1 (Entity 1) - MV2 (Entity 2) = 0.00c. The Entities would
neither approach nor depart from each other.
Because inre the minimum RV the entities are not moving inre each
other, then the minimum RV
equation is RV = MV1 ± MV2 = 0.00c ± 0.00c = 0.00c, e.g.
RV = MV1 + MV2 = 0.00c + 0.00c = 0.00c and RV = MV1 - MV2 = 0.00c -
0.00c = 0.00c.
Velocities inre Einstein's Fig. 1
Fact: Inre Einstein's Fig. 1, Lightray B' approaches M' at an ARV that
is the combination of the sum of the MV1 of
Lightray B' and the MV2 of M' given by ARV = MV1 + MV2.
Fact: Inre Einstein's Fig. 1, Lightray A' approaches M' at an ARV that
is the difference between the MV1 of
Lightray A' and the MV2 of M' given by ARV = MV1 - MV2.
The Einstein light motion relative velocity
equation, ...
RV = (MV1 + MV2)/(1 + MV1 x MV2/c2
... always produces the result RV = 1.00c, which fits the relativistic
claim that the
speed of light is the same for all observers.
If the Einstein light motion relative velocity equation always produces
the result of RV = 1.00c, which is implied in Chapter XIII, then it is not possible for the Einstein light
motion relative velocity equation
to describe accurately the ARV inre Lightray A' and M' nor the ARV inre
Lightray B' and M' because of the description of the RVs inre Lightrays
A' & B' inre M' given by Einstein in Paragraph 3 and by paraphrases
of Einstein's Paragraph 3 in my Sequence
1, Sequence 1b and Sequence 1c, and animated in Movie 1c, wherein M'
approaches Lightray B'
and is struck by Lightray B' before being struck by Lightray A', and
Lightray A' approaches M' and strikes him after he has been struck by
Lightray B'.
When M' is traveling at an unspecified MV2 parallel to and towards
Lightray B' which is traveling at MV1 = 1.00c parallel to M' but in the
opposite direction, then M' has an MV2 which has to be added to the MV1
of Lightray B' via RV = MV1 + MV2.
As observed from reference frame K/the Embankment, the ARVs inre
Lightrays A & B inre M are 1.00c but the
ARVs inre Lightrays A' & B' inre M' inre reference frame K'/the
Train are not 1.00c.
ARV = MV1 ± MV2 gives the correct ARVs inre Lightrays A' &
B'
inre M' as well as the correct ARVs inre Lightrays A & B inre M but
although RV = (MV1 + MV2)/(1 + MV1 x MV2/c2 gives the
correct RVs
inre
Lightrays A & B inre M it does not
give the correct ARVs inre
Lightrays A' & B' inre M'.
Relative Velocities and the Einstein
Light Motion Paradox
Inre Einstein's Fig. 1, because of the fact that ARV = MV1 ± MV2
gives the correct ARVs
inre Lightrays A' & B' inre M' but RV = (MV1 + MV2)/(1 + MV1 x MV2/c2
does not give the correct ARVs
inre Lightrays A' & B' inre M', we
have the Einstein Light Motion Paradox.
Simultaneity
and The General Principle of Relativity
The general
principle of relativity states describes the fact that the laws
of physics are the same for any reference frame or reference body.
Einstein's theory of relativity depends upon laws of physics in one
reference frame or on
one reference body being the same in any and all other reference frames
or on any and all other reference bodies.
Inre Fig. 1 of Chapter IX of Relativity,
in Paragraph 3, Einstein stated that, as M would observe from reference
frame K (in which are located M & the Embankment), the following
sequence occurred:
Sequence 1
1. Lightning strikes A & B; Events A & B occur simultaneously
inre distance A-B
inre both the Embankment &
the Train;
2. Lightray B' from Event B' strikes M' (M' reports detecting light
from Event B');
3. Lightrays A & B from Events A and B strike M (M reports
detecting light from Events A
and B and his judgment that Events A & B occurred simultaneously);
4. Lightray A' from Event A' strikes M' (M' reports detecting light
from Event A'
and his judgment that Events A' & B' occurred non-simultaneously).
When timepoints T1, T2, T3, & T4 are added to Sequence 1, we get
Sequence 1b:
Sequence 1b
1. T1: Lightning strikes A & B; Events A & B occur
simultaneously inre distance A-B
inre BOTH the Embankment & the Train;
2. T2: Lightray B' from Event B' strikes M' (M' reports detecting light
from Event
B);
3. T3: Light from A and B strike M (M reports detecting light from
Events A
and B and his judgment that Events A & B occurred simultaneously);
4. T4: Lightray A' from Event A' strikes M' (M' reports detecting light
from Event
A' and his judgment that Events A' & B' occurred
non-simultaneously).
According to the general principle of relativity, from reference frame
K' (in which are located M' & the Train), M' should observe
Sequences 1 and1b inre reference frame K and M and the Embankment:
Sequence 1 (As observed by M' from reference frame K')
1. Lightning strikes A & B; Events A & B occur simultaneously
inre distance A-B
inre BOTH the Embankment & the Train;
2. Lightray B from Event B strikes M (M reports detecting light from
Event B);
3. Lightrays A' & B' from Events A' and B' strike M' (M' reports
detecting light from Events A'
and B' and his judgment that Events A' & B' occurred
simultaneously);
4. Lightray A from Event A strikes M (M reports detecting light from
Event A
and his judgment that Events A & B occurred non-simultaneously).
Sequence 1 (As observed by M' from reference frame K')
1. T1: Lightning strikes A & B; Events A & B occur
simultaneously
inre distance A-B
inre BOTH the Embankment & the Train;
2. T2: Lightray B from Event B strikes M (M reports detecting light
from Event B);
3. T3: Lightrays A' & B' from Events A' and B' strike M' (M'
reports detecting light from Events A'
and B' and his judgment that Events A' & B' occurred
simultaneously);
4. T4: Lightray A from Event A strikes M (M reports detecting light
from Event A
and his judgment that Events A & B occurred non-simultaneously).
Note that, according to the general principle of relativity, by simply
exchanging the symbol M' for M in Sequences 1 & 1b we get the same
results: the observer (M or M') in the reference frame that is supposed
to be at-rest will observe that he will detect Lightrays from Events A
& B (or Events A' & B') simultaneously, at the same timepoint,
and thereby he can judge and report that Events A & B (or Events A'
& B') occurred simultaneously while he supposedly will observe that
the other observer in the reference frame that is supposed to be moving
will detect one Lightray from Event A or B (or Event A' or B') before
detecting the other Lightray from the other Event and supposedly will
judge and report that Events A & B (or Events A' & B') did NOT
occur simultaneously.
Because (P) we have two reference frames and either could be the
at-rest or the moving reference frame and therefore either
observer (M
or M') could be the at-rest observer while the other is the moving
observer, then (Q) we therefore have two possibilities for two
conflicting judgments and reports: (1) The observer in the at-rest
reference frame will judge and report Events A & B (or Events A'
& B') occurred simultaneously but (2) the observer in the moving
reference frame will judge and report that Events A & B (or Events
A' & B') did NOT occur simultaneously.
There is a problem herein: If we disregard the concept of the general
principle of relativity wherein the relationships observed from one
reference frame by observers in that reference frame should also be
observed from another reference frame by observers in that reference
frame, a fact which could produce conflicting observations,
measurements and reports inre WIGO inre the relationships, there is a
possibility a relationship, such as the simultaneity of events, can be
determined objectively, without the viewpoint (point-of-view, or PoV)
of an oberver in either of the reference frames.
We could use the concept and relevant principles of time
to create the physical evidence which would serve as proof of the
simultaneities of events, as well as the sequences of events, the
causalities of events, and the changerates (rates of change) of events
inre different reference frames/bodies.
The Concept of Time
Time is the combination of The Temporal Principle and The Temporal Process.
The Temporal Principle
The Temporal
Princple: Time is the
use of a chosen duration (recurring event, cycle, or a model of a
chosen duration) to be used as a time-interval to be used as the unit
of temporal meaurement for the measurement of the durations between the
occurrences of events, the durations of single events, and the
durations (ages) of people and objects, and for the generation in
timepieces (clocks, watches, etc.) of their timerates (rates of
ticking, RoTs, tick-rates), timepoints (marks on a timeline), timelines
(histories, records of timepoints, continuums of time), and timecounts
(accumulations of timepoints inre a timeline, by addition, from a
chosen timepoint origin, T0, from the past through the present into the
future, with the arrow of time pointing from the past through the
present into the future), and for the determination of the sequences,
the simultaneities, the causalities, and the changerates of events, or
for the coordination (synchronization) of events, inre single or
multiple reference frames/bodies.
The Time-Interval
A time-interval
(TI) is a chosen duration which can be modeled after a physical
recurring event, periodic motion, or cycle, or modeled from an
abstracted duration.
Ex: The standard second is the duration of 9b c-atom oscillations at
the Earth's surface.
Ex: Mechanical clocks could mimick or imitate the 9b c-atom oscillation
duration b/c that 9b c-atom oscillation can be abstracted when
designers and fabricators set the mechanical clock's timerate to match
that, be identical to, the timerate set by the duration of the 9b
c-atom oscillations.
The Timerate
A timerate is the rate of ticking (RoT), the rate of operation (RoO),
the rate of functioning (RoF), of a timepiece (watch, clock, etc.).
For temporal accuracy, the durations between the ticks of a clock
should be equal, and the durations of the ticks should also be equal.
Timepoints
A timepoint
is a mark inre a timeline.
For mechanical clocks, a timepoint is a number on the clock's face;
when the hour, minute, and second hands of a mechanical clock move,
their positions determine the clock's timepoints.
For digital clocks, a timepoint is the timepoint which shows in the
clock's readout or display.
Timepoints occur inre timelines.
Timelines
A timeline
is a record, history or continuum of time, a list of timepoints.
At each timepoint on a timeline, there is a unique configuration of the
universal m/e system (matter-energy system); thus, there is a
combination of a unique/specific timepoint and a unique/specific m/e
configuration which, together, as a combination, occur once in the
history/timeline of the universe and never again.
A timeline is dated from a chosen timepoint, T0, which is a chosen
origin.
A timeline can be a uni-directional timeline
(single direction timeline) or a bi-directional timeline
(double direction timeline)
A uni-directional
timeline begins at a chosen origin timepoint, T0, and is counted
forward from that T0.
T0 -> T+1 -> T+2 -> ... ->
Infinity Future
A bi-directional
timeline begins at a chosen timepoint origin, T0, and is counted
backwards and forwards from T0.
Past Infinity <- ... <- T-2
<- T-1 <- T0 -> T+1 -> T+2 -> ... -> Infinity Future
Despite the fact that there are two types of continuums of time,
uni-directional and bi-directional, new, unique, timepoints are always
accumulated in the future from the past and the present.
Therefore, the timepoints on the timeline of the universe have
accumulated from the past through present and will accumulate from the
present into the future.
Thus, there is an arrow-of-time which always and only "travels" from
the past through the present into the future.
The uniqueness of each timepoint & m/e configuration means that
timepoint & m/e combination, regardless of when/where on the
universal timeline it occurred, will never occur again.
Ex: You, and I, as we are at this present timepoint and within the
present universal m/e configuration, are in a unique timepoint &
m/e combination, have changed in past timepoint & m/e combinations
and will change inre future timepoint & m/e combinations, and
whereas today we are not what we were yesterday tomorrow we will not be
what we are today, and therefore we will never be as we were.
The fact that a unique timepoint & m/e combination occurs once on
the universal timepoint means time travel is impossible.
Timecounts
A timecount
is the accumulation, by addition, of the timepoints on a timeline.
To determine a timecount, such as a duration between events, or the
duration of a single event, a timepoint origin must be chosen in order
for timepoints to accumulate by addition from that timepoint origin to
the present timepoint.
Ex: The timecount for a mechanical clock is the change from a previous
hand alignment inre the clock's face numbers to the present hand
alignment inre the clock's face numbers, always clockwise; timekeepers
will have to do mentally or manually the calculations of timepoints
from the previous hand alignment to the current or anticipated hand
alignment.
Ex: The timecount for a digital clock is the change from a previous
readout to the present readout, which is always larger/greater than the
previous readout; timekeepers will have to do mentally or manually the
calculations of
timepoints from the previous readout to the current or
anticipated readout.
When timepoint origins are marked on a timeline, the accumulation of
timepoints becomes a line of marks from the timepoint origin to the
present timepoint.
The Temporal Process
The Temporal
Process: Time is the use
of a chosen duration for the time-interval which is to be the unit of
temporal measurement for the design, fabrication and deployment of
timepieces which are to have designed timerates, timepoints, timelines,
and timecounts to be used for the temporal measurement process for the
measurement of the durations between the
occurrences of events, the durations of single events, and the
durations (ages) of people and objects, and for the generation in
timepieces (clocks, watches, etc.) of their timerates (rates of
ticking, RoTs, tick-rates), timepoints (marks on a timeline), timelines
(histories, records of timepoints, continuums of time), and timecounts
(accumulations of timepoints inre a timeline, by addition, from a
chosen timepoint origin, T0, from the past through the present into the
future, with the arrow of time pointing from the past through the
present into the future), and for the determination of the sequences,
the simultaneities, the causalities, and the changerates of events, or
for the coordination (synchronization) of events, inre single or
multiple reference frames/bodies.
Thus, time is the combination of the Temporal Principle and the
Temporal Process.
---
All biologicals including human biologicals must use the temporal
principle to "do time", i.e. to engage in the temporal process. That
means space aliens, if they exist, would have to use the temporal
principle to create timepieces to engage the temporal process.
All machines, especially computers, are designed to incorporate the
temporal principle into the temporal processes they need to operate as
designed.
Time: Never Destroyed nor Created
Time is never destroyed nor created.
Ex: If you drop your watch and it no longer functions as designed,
then, although the temporal process inre that watch is destroyed, time
is not destroyed because the principle of time is never destroyed, and
the principle of time means you can once again engage the temporal
process by repairing your watch or by buying another watch.
By being never created nor destroyed, time, as the temporal principle,
has always been, is now, and forever will be, a universal reality from
the past through the present into the future.
Time: Infinite in Duration
As the temporal principle, time is indestructible, and infinite in
duration.
The Essence of Time: The Time-Interval
The essence of time is the time-interval—the
chosen duration which is the unit of temporal measurement.
There are two types of time-intervals: (1) the distortable time-interval, or d-time-interval,
whose duration is distorted by accelerations and decelerations, whose
duration is increased by accelerations and whose duration is decreased
by decelerations; (2) the adjustable
time-interval, or a-time-interval,
whose duration is not
distorted by accelerations or decelerations
because it (the a-time-initerval's duration) is adjusted to maintain a
pre-set or original duration.
The Two Types of Clocks
There are two types of clocks: (1) distortable
clocks, d-clocks,
whose timerates (tick-rates, rates of ticking) are distorted by
accelerations and decelerations, wherein accelerations cause decreases
in d-clocks' timerates and decelerations cause increases in d-clocks'
timerates, and (2) adjustable clocks,
a-clocks,
whose timerates are not
distorted by accelerations and decelerations
because their timerates are adjusted to maintain a pre-set original
timerate despite accelerations and decelerations so the a-clocks
essentially are "independent of the state of motion of [their bodies]
of reference" [Einstein, Relativity,
1961 edition, p. 27]. Thus, when the state of motion of the body of
reference of a d-clock is changed by acceleratons or decelerations, the
d-clock's timerate is changed, but when the state of motion of the body
of reference of an a-clock is changed by accelerations or
decelerations,
the a-clock's timerate is essentially unchanged.
D-clocks are also called local time clocks
(LTCs); a-clocks are also called absolute time clocks
(ATCs)
The Two Types of Time
A d-clock essentially measures distortable
time, or d-time, or local time, or l-time—the time for a single unique
reference frame/body, whereas an a-clock thereby measures absolute time or a-time—the universal time for
multiple different reference frames/bodies.
Thus, there are two types of time: (1) distortable time, d-time, which
is also local time, l-time; (2) absolute time, a-time.
Distortable Time: Local Time
Distortable
time, or d-time,
or local time,
or l-time is the time for a single unique
reference frame/body generated by the timerates, timepoints, timeines,
and timecounts of distortable clocks, d-clocks, or local time clocks
(LTCs).
D-time changes when d-clocks are accelerated or decelerated.
Accelerations and decelerations cause distortions of the mechanisms of
mechanical clocks and distortions of the oscillations of digital clocks
which result in distortion of the d-clocks' timerates, timppoints,
timelines, and timecounts.
The Continuum of Local Time (CoLT)
A continuum of local time (d-time) can be created by either a
uni-directional timeline or a bi-directional timeline.
A local time or
d-time uni-directional timeline is unique, specific, to a single
reference frame/body and begins at a chosen origin timepoint, T0, and
is counted forward from that T0.
T0 -> T+1 -> T+2 -> ... ->
Infinity Future
A local time or
d-time bi-directional
timeline is unique, specific, to a single reference frame/body
and begins at a chosen timepoint origin, T0, and is counted backwards
and forwards from T0.
Past Infinity <- ... <- T-2
<- T-1 <- T0 -> T+1 -> T+2 -> ... -> Infinity Future
A CoLT will distort as its d-clock and/or its d-clock's reference body
is accelerated or decelerated.
Adjustable/Non-Distortable Time:
Absolute Time
Absolute time
or a-time,
or absolute time,
also a-time,
is the universal time for
multiple different reference frames/bodies generated y the timerates,
timepoints, timelines, and timecount of adjustable clocks, a-clocks,
also non-distortable clocks, nd-clocks, also asbslute time clocks (ATCs)
The Continuum of Absolute Time (CoAT)
A continuum of absolute time (a-time) can be created by either a
uni-directional timeline or a bi-directional timeline.
An absolute time
or a-time uni-directional timeline
is universal to all reference frames/bodies and begins at a
chosen origin timepoint, T0, and is counted forward from that T0.
T0 -> T+1 -> T+2 -> ... ->
Infinity Future
An absolute time
or a-time bi-directional
timeline
is universal to all reference frames/bodies and begins at a
chosen timepoint origin, T0, and is counted backwards and forwards from
T0.
Past Infinity <- ... <- T-2
<- T-1 <- T0 -> T+1 -> T+2 -> ... -> Infinity Future
A CoAT will not distort as its a-clock
and/or its a-clock's reference body is accelerated or decelerated
because the a-clock is designed to be adjusted (radio a-clock) or
adjust itself (inertial a-clock) to compensate for the distortions
caused by acceerations and decelerations.
The Two Types of Adjustable Clocks:
Radio Clocks & Inertial Clocks
There are two types of a-clocks: (1) radio
a-clocks, wherein a master clock sends radio signals to slave
clocks and thereby controls the slave clocks' timerates; (2) inertial a-clocks,
wherein accelerometers detect changes of the state of motion (inertial
state) of the body of reference (the body of reference being either the
a-clock or the Entity upon which the a-clock is at-rest) and computers
adjust the inertial a-clocks' timerates.
For the measurement of absolute time, an a-clock must tick with equal
time-intervals—equal durations—between ticks and equal
time-intervals—equal durations—of ticks.
A clock-tick will have a duration. That duration can be measured by the
chosen
time-interval.
There will be a duration between clock-ticks. That duration can be
measured
by the chosen time-interval.
Moreover, an a-clock must continue to tick at the same timerate
(tickrate) despite accelerations and decelerations which would cause
timerate changes in d-clocks. This means an a-clock must be
"independent of the state of motion of the body of reference"
[Einstein, Relativity, 1961
edition, p. 27]. This means an
a-clock must be independent of inertial state changes inre whatever
reference body upon which or within which it is located. This means
that if an a-clock is located/positioned within a spaceship, then the
a-clock must function in such a way that its timerate remains
steady and thus must be independent of the spaceship's inertial state
changes caused by accelerations and/or decelerations inre the
spaceship. The design and fabrication of a-clocks causes both radio
clocks and inertial clocks to function independently of the state of
motion of their bodies of reference in accord with Einstein's a-clock
requirements.
Radio
Clocks
In the radio clock design, a master clock sends radio signals to slave
clocks and thereby controls the slave clocks' timerates, timepoints,
timelines, and timecounts.
Radio a-clocks are in-use as the standard clocks which generate the
standard second and which are in-use by the USNO (United States Naval
Observatory), the US NIST (US National Institute of Standards and
Technology) and and the BIPM (Bureau Internationale des Poids et
Mesures) and for the US GPS (United States Global Positioning
Satellite) navigation system (which uses a master clock which is
synched to the USNO standard clocks). Thus, radio clocks are realities.
The operation of a radio clock depends on the stability of the
reference body upon which the radio clock is located/positioned. So
long as a radio clock's reference body is not accelerated or
decelerated and thus its inertial state is unchanged and therefore the
reference body and the radio clock is stable, then the radio clock will
continue to function as designed. So long as the Earth is stable inre
its rotation about its axis and its orbit about the Sun and the Sun's
orbit about anything else in the universe, then a radio clock on the
Earth's surface will continue to measure absolute time, a-time.
Inertial Clocks
In the inertial clock design, accelerometers detect changes of the
state of motion (inertial
state) of the body of reference (the body of reference being either the
a-clock or the Entity upon which the a-clock is at-rest) and computers
adjust the inertial a-clocks' timerates.timepoints, timelines, and
timecounts.
Inertial a-clocks are in-use by the US Military for inertial navigation
systems for aircraft, ships, and submarines; in the US Military, an
onboard
inertial navigation system is called the INS.
The operation of an inertial clock is independent of the state of
motion (inertial state) and/or stability of its reference body upon
which the inertial clock is located/positioned. Inherent in the design
of an inertial clock is the independence of the clock from the state of
motion of any reference body upon which it is located/positioned.
Accelerations and/or decelerations of an inertial clock's reference
frame will be automatically detected by the inertial clock's
accelerometers and the clock's computer will automatically adjust the
clock's timerate to maintain the clock's pre-set/original timerate and
timepoints, timeline, and timecount.
Simultaneities, Timepoints, and
Time-Stamps
If we could use a-clocks to measure a-time and time-stamp photos or
videos of events taken by cameras linked and synched to the a-clocks,
then identical time-stamps of photos or videos of events would be the
physical evidence that would be the proof that could be used to
determine the simultaneities of events.
If we were to use camera and a-clock combinations to photograph or
videorecord and time-stamp Events A & B (or/and Events A' & B')
inre Fig. 1, then the timestamps would determine the simultaneity of
Events A & B (or Events A' & B') without, or regardless of,
judgments from M or M'. These time-stamped proofs would be independent
of the observations, measurements, and judgments of observers inre
different reference frames/bodies. These time-stamped proofs would
prove
that Events A & B (and Events A' & B') occurred
simultaneously—at the same a-clock timepoint.
These time-stamped photos/videos would destroy the relativity of
siimultaneity. No one would care what M or M' detected, judged or
concluded from K or K' inre the light motions of Fig. 1.
The Moving Observer Illusion (MOI)
In Paragraph 2 inre Fig. 1 of Chapter IX of Relativity, Einstein stated that
Events A & B occurred simultaneously inre both the Embankment and
the Train. He needed Events A & B to occur simultaneously inre both
the Embankment and the Train for the phenomena wherein (A) M is struck
simultaneously—at the same timepoint—by Lightrays A & B and (B) M'
is struck non-simultaneously—at different timepoints—by Lightrays A'
& B' from Events A' & B'.
Einstein also needed the length A-B inre the Embankment to be the same
physical length as length A'-B' inre the Train.
Clarification: If (P) identical a-clocks are used for the
definition of time and the temporal measurement inre both the
Embankment and the Train, then, because their time-intervals—their
units
of temporal measurement—will be identical, (Q) the timerates,
timepoints, timelines, and timecounts of all identical a-clocks
will be identical and therefore simultaneity, two or more events
occurring at the same timepoint, can be defined and determined by the
use of the identical a-clock timepoints and timeline.
Timepoint T1 inre the Embankment is identical to timepoint T1 inre the
Train.
Thus, when (P) Events A & B occur at timepoint T1 inre the
Embankment, then (Q) Events A & B also occur at timepoint T1 inre
the Train. Thus, Events A & B are simultaneous—Events A & B
occur simultaneously—inre both
the Embankment and the Train.
If (P1) M' reports that because (P2) Lightrays A' & B' did not
strike him at the same timepoint then (Q2) Events A & B did not
occur simultaneously, then (Q1) is reporting a false claim—an
illusion—because of the fact that Events A & B occurred
simultanesouly—at the same timepoint—inre both the Embankment and the
Train.
This illusion occurs because M' is moving inre Lightrays A' & B'.
In Paragraph 3 of Chapter IX of Relativity,
Einstein is specific inre the motions of Lightrays A' & B' inre M':
M' is moving towards Lightray B' and away from Lightray A'.
This fact means there is an RV difference inre the motion of Lightray
A' inre M' and the motion of Lightray B' inre M'.
This RV difference can only be
described by RV = MV1 ± MV2.
This illusion can be called the moving observer illusion (MOI). The MOI
is apparent when
lightrays have different directions of motion inre an observer and are
therefore moving at different RVs inre the observer.
Summary: The
Einstein Light Motion Paradox
Inre Einstein's Fig. 1 drawing from Chapter IX of Relativity, 1961 edition, there are
two mutually exclusive possibilities:
Either ...
... (A) Light travels at ...
RV = MV1 ± MV2
... inre observers and objects who/which are in-motion at an AV >
0.00c or otherwise are at-rest at an AV = 0.00c and therefore the
causal and coincidental relationships inre light motion, M, the
Embankment, M' and the Train are as Einstein himelf described in
Chapter IX and as summarized in Sequence 1, ...
Sequence 1
1. Lightning strikes A & B; Events A & B occur simultaneously
inre distance A-B
inre both the Embankment &
the Train;
2. Lightray B' from Event B' strikes M' (M' reports detecting light
from Event B');
3. Lightrays A & B from Events A and B strike M (M reports
detecting light from Events A
and B and his judgment that Events A & B occurred simultaneously);
4. Lightray A' from Event A' strikes M' (M' reports detecting light
from Event A'
and his judgment that Events A' & B' occurred non-simultaneously).
... and in Sequence 1b, ...
Sequence 1b
1. T1: Lightning strikes A & B; Events A & B occur
simultaneously inre distance A-B
inre BOTH the Embankment & the Train;
2. T2: Lightray B' from Event B' strikes M' (M' reports detecting light
from Event
B');
3. T3: Lightrays A & B from Events A and B strike M (M reports
detecting light from
Events A
and B and his judgment that Events A & B occurred simultaneously);
4. T4: Lightray A' from Event A' strikes M' (M' reports detecting light
from Event
A' and his judgment that Events A' & B' occurred
non-simultaneously).
... and in Sequence 1c ...
Sequence
1c
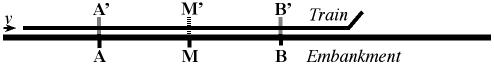
1. T1: Events A & B Occur Simultaneously inre the Embankment and
the
Train.

2. T2: Lightray B' from Event B Strikes M'.

3. T3: Lightrays A & B from Events A & B Strike M.

4. T4: Lightray A' from Event A Strikes M'.
... or ...
... (B) Light travels at ...
RV = (MV1 + MV2)/(1 + MV1 x MV2/c2)
= 1.00c
... inre observers and objects who/which are in-motion at an AV
>
0.00c or otherwise are at-rest at an AV = 0.00c and therefore the
causal and coincidental relationships inre light motion, M, the
Embankment, M' and the Train are as described and summarized in
Sequence 2, ...
Sequence 2
1. Events A & B occur simultaneously inre the Embankment and the
Train.
2. Lightrays from A & B strike M and M' simultaneously (both M
& M'
report detecting Lightrays from Events A & B simultaneously and
their judgments that Events A & B occurred simultaneously).
NOTE: Because Lightrays from A &
B
struck M and M' simultaneously, there is no need for a T3 or a T4 inre
Sequence 2.
... and in Sequence 2b ...
Sequence 2b.
1. T1: Events A & B occur simultaneously inre the Embankment and
the
Train.
2. T2: Lightrays from Events A & B Strike M and M' Simultaneously
(Both M
& M' report detecting Lightrays from Events A & B
simultaneously and their judgments that Events A & B occurred
simultaneously).
NOTE: Because Lightrays from A &
B
struck M and M' simultaneously, there is no need for a T3 or a T4 inre
Sequence 2b.
... and in Sequence 2c ...
Sequence
2c
1. T1: Events A & B Occur
Simultaneously Inre The Embankment And The Train.

2. T2: Lightrays from A & B Strike M and M' Simultaneously.
Light cannot travel at
both ...
(A) RV = MV1 ± MV2 ≠ 1.00c
...
and ...
(B) RV = (MV1 + MV2)/(1 + MV1 x MV2/c2).
The
Einstein Light Motion Paradox: Einstein claimed inre Fig. 1 of
Chapter IX of
Relativity that
light can travel at (A) RV = MV1 ± MV2
and he also claimed in
Chapter XIII of
Relativity
that light can travel at (B) RV = (MV1 + MV2)/(1 + MV1 x MV2/c
2).